Μήνας: Σεπτέμβριος 2022
Ανακοίνωση σχετικά με τη χορήγηση πιστοποιητικών
Συνημμένo Έντυπo:
Υποτροφίες για υποψήφιους Διδάκτορες, Καθηγητές και Ερευνητές από την Σλοβακία
Συνημμένo Έντυπo:
Ανακοίνωση σχετικά με τη χορήγηση βεβαίωσης παιδαγωγκής επάρκειας σύμφωνα με τις διατάξεις του Ν.4957/22
Συνημμένo Έντυπo:
Πρόγραμμα διδασκαλίας μαθημάτων χειμερινού εξαμήνου ακαδημαϊκού έτους 2022-23
Μπορείτε να κατεβάσετε το Ωρολόγιο Πρόγραμμα Διδασκαλίας Μαθημάτων μετά τις παρακάτω αλλαγές (Ημερ. Τροποποίησης: 12/10/2022).
| A/A | ΠΡΟΓΡΑΜΜΑ ΔΙΔΑΣΚΑΛΙΑΣ ΜΑΘΗΜΑΤΩΝ – ΙΣΤΟΡΙΚΟ ΑΛΛΑΓΩΝ | ΑΡΧΕΙΑ/ΑΝΑΚΟΙΝΩΣΕΙΣ |
| 1. | Αρχικό πρόγραμμα διδασκαλίας μαθημάτων χειμερινού εξαμήνου ακαδημαϊκού έτους 2022-23 (Ημερ. δημοσίευσης: 28/09/2022) | |
| 2. | Ανακοίνωση για τη διάλεξη του μαθήματος “Τεχνητή Νοημοσύνη” την Τρίτη 4 Οκτωβρίου 2022 | Αρχείο |
| 3. | Ανακοίνωση για τη διάλεξη του μαθήματος “Δομές Δεδομένων” την Δευτέρα 10 Οκτωβρίου 2022 | Αρχείο |
| 4. | Συμμετοχή φοιτητών 1ου και 3ου εξαμήνου σπουδών στα εργαστηριακά μαθήματα χειμερινού εξαμήνου 2022-23 | Ανακοίνωση |
| 5. | Ανακοίνωση για τη διάλεξη του μαθήματος “Εκπαιδευτική Ψυχολογία” την Πέμπτη 6 Οκτωβρίου 2022 | Αρχείο |
| 6. | Προθεσμία για δηλώσεις μαθημάτων χειμερινού εξαμήνου ακαδημαϊκού έτους 2022-23 | Ανακοίνωση |
| 7. | Αλλαγή ημέρας και αίθουσας διδασκαλίας του μαθήματος του 7ου εξαμήνου “Συστήματα Ευφυών Πρακτόρων” | Ανακοίνωση |
| 8. | Δήλωση δευτερεύουσας κατεύθυνσης (ΥΠΟ κατεύθυνσης) στο 7ο εξάμηνο σπουδών (αφορά τα μητρώα, Ε/18, Ε/17, Ε/16, Ε/15 που δεν έχουν δηλώσει δευτερεύουσα κατεύθυνση τα προηγούμενα έτη) | Ανακοίνωση |
| 9. | Οδηγίες για τη δήλωση Δευτερεύουσας Κατεύθυνσης στο 7ο εξαμηνο σπουδών (αφορά τα μητρώα Ε/19) | Ανακοίνωση |
| 10. | Διαδικασία δήλωσης και διανομής συγγραμμάτων χειμερινού εξαμήνου ακαδημαϊκού έτους 2022-2023 | Ανακοίνωση |
| 11. | Οδηγίες Εγκατάστασης “MatLab” (επικαιροποιημένος οδηγός εγκατάστασης της εφαρμογής – ΟΚΤΩΒΡΙΟΣ 2022) | Αρχείο |
| 12. | Παράταση προθεσμίας δηλώσεων μαθημάτων χειμερινού εξαμήνου ακαδημαϊκού έτους 2022-23 | Αρχείο |
| 13. | Ανακοίνωση αναβολής μαθημάτων 2-11-2022 (ώρες 11:00 με 15:00) | Ανακοίνωση |
Πρόσκληση παρουσίασης διδακτορικής διατριβής κας Ελένης-Λασκαρίνας Μακρή
Συνημμένo Έντυπo:
Ευρωπαϊκό Έτος Νεολαίας 2022
Ergodic Capacity of Generalized Fading Channels with Mobility
V. A. Aalo, P. S. Bithas and G. P. Efthymoglou, “Ergodic Capacity of Generalized Fading Channels With Mobility,” in IEEE Open Journal of Vehicular Technology, vol. 3, pp. 15-25, 2022, doi: 10.1109/OJVT.2021.3131321.
Χωρητικότητα (capacity, C) μίας τηλεπικοινωνιακής σύνδεσης με φάσμα εκπομπής BW (Hz) είναι ο μέγιστος ρυθμός πληροφορίας R_bit σε bit/sec. Συνήθως ορίζουμε την χωρητικότητα ανά μονάδα εκπεμπόμενου φάσματος ως το πηλίκο C/BW σε bit/sec/Hz. Σύμφωνα με το θεώρημα του Shannon η χωρητικότητα ενός καναλιού (μίας σύνδεσης) εξαρτάται από το σηματοθορυβικό λόγο λήψης (received signal-to-noise ratio, SNR), με βάση τον τύπο C=BW*log2(1+SNR). To SNR λήψης στον δέκτη είναι το πηλίκο της λαμβανόμενης ισχύος σήματος προς την ισχύ του θορύβου στην κεραία του δέκτη. Η λαμβανόμενη ισχύς σήματος εξαρτάται από την απόσταση πομπού-δέκτη και υπολογίζεται με βάση κάποιο μοντέλο διάδοσης. Το πιο απλό αλλά και σχετικά αξιόπιστο μοντέλο διάδοσης είναι αυτό στο οποίο η μείωση της ισχύος είναι αντιστρόφως ανάλογη της απόστασης υψωμένης σε μία δύναμη η, όπου παράμετρος η, 2<η<6, ονομάζεται path loss exponent. Η τιμή της παραμέτρου η εξαρτάται από το περιβάλλον διάδοσης μεταξύ πομπού και δέκτη. Με βάση αυτό το μοντέλο διάδοσης μπορούμε να υπολογίσουμε για κάποια απόσταση d μεταξύ πομπού-δέκτη την μέση λαμβανόμενη ισχύ ως P_r(d)=P_t*d^(-η)*((λ/(4π))^2), όπου P_t είναι η ισχύς εκπομπής και λ το μήκος κύματος του φέροντος εκπομπής. Στη συνέχεια μπορούμε να βρούμε το μέσο λαμβανόμενο SNR για απόσταση d ως SNR(d)=P_r(d)/N, όπου Ν η ισχύς του θορύβου, και τέλος το μέγιστο bit rate ανά μονάδα φάσματος που μπορεί να επικοινωνεί ο δέκτης με βάση την παραπάνω σχέση του Shannon.
Στα ασύρματα κανάλια επικοινωνίας η στιγμιαία λαμβανόμενη ισχύς σήματος (και κατ’ επέκταση το στιγμιαίο λαμβανόμενο SNR) δίνεται από την μέση λαμβανόμενη ισχύ (η οποία εξαρτάται αποκλειστικά από την απόσταση και την παράμετρο path loss exponent) πολλαπλασιασμένη με την ισχύ του καναλιού |h|^2, ως SNR=P_r(d)*|h|^2. Η ισχύς του καναλιού ορίζεται ως το μέτρο στο τετράγωνο του συντελεστή του καναλιού h, ο οποίος χαρακτηρίζει το φαινόμενο της διάλειψης (fading) που υφίσταται το σήμα λήψης στο ασύρματο κανάλι. Στην βιβλιογραφία υπάρχουν πολλές κατανομές που δίνουν τη στατιστική περιγραφή του συντελεστή διάδοσης ενός ασύρματου καναλιού, όπως προκύπτουν είτε από ταίριασμα συναρτήσεων πυκνότητας πιθανότητας (probability density functions, PDFs) σε πειραματικές μετρήσεις που γίνονται σε διάφορα περιβάλλοντα μετάδοσης και διάφορες συχνότητες φερόντων (carrier frequencies) είτε με βάση φυσικά μοντέλα διάδοσης τα οποία όμως επαληθεύονται από πειραματικά δεδομένα. Η πιο χαρακτηριστική PDF δίνεται από τη συνάρτηση Rayleigh η οποία θεωρεί ότι το σήμα λήψης είναι η συνισταμένη πολλών ανακλώμενων και διαθλώμενων διαδρομών του σήματος εκπομπής με απουσία απευθείας διαδρομής. Η Rayleigh PDF έχει επαληθευτεί με διάφορες μετρήσεις σε κινητούς δέκτες σε περιβάλλοντα χωρίς οπτική επαφή πομπού-δέκτη. Την τελευταία δεκαετία έχουν αναφερθεί στη βιβλιογραφία πολλές ακόμα PDFs που δίνουν το στατιστικό χαρακτηρισμό του συντελεστή του καναλιού για διαφορετικά περιβάλλοντα διάδοσης αλλά και διαφορετικές συχνότητες φέροντος (π.χ. 800 ΜΗz, 3.5 GHz, 27 GΗz, κτλ), όπως η Nakagami-m, Generalized-K, α-μ, η-μ, κ-μ, α-η-μ, α-κ-μ και α-κ-μ shadowed.
Στην περίπτωση λήψης σήματος με διάλειψη σε σταθερή απόσταση d πρέπει να βρούμε το στατιστικό μέσο όρο (statistical average) της χωρητικότητας του καναλιού για μέσο λαμβανόμενο SNR(d) ως προς την κατανομή της ισχύος του καναλιού |h|^2. Για κάθε μια από τις παραπάνω PDFs του συντελεστή του καναλιού h έχουν βρεθεί μαθηματικές σχέσεις για την χωρητικότητα του καναλιού, ώστε κάποιος να μπορεί γρήγορα να υπολογίσει το μέγιστο bit rate συναρτήσει του μέσου SNR για διαφορετικά περιβάλλοντα διάδοσης. Τα αποτελέσματα αυτά θεωρούν δέκτη σε συγκεκριμένη θέση, άρα σταθερή απόσταση πομπού-δέκτη, ο οποίος λαμβάνει το σήμα με διάλειψη λόγω της διάδοσης στο ασύρματο κανάλι.
Στο συγκεκριμένο άρθρο θεωρούμε ότι ο δέκτης κινείται μέσα σε μία περιοχή με ακτίνα D, η οποία ορίζει την περιοχή κάλυψης (coverage area) ενός σταθμού βάσης. Με βάση την μέγιστη απόσταση πομπού-δέκτη D και το μοντέλο διάδοσης ορίζουμε το μέσο SNR στο όριο της περιοχής κάλυψης SNR_D=P_t*D^(-η)/Ν. Ως μοντέλο κίνησης θεωρούμε το random waypoint (RWP) model για το οποίο γνωρίζουμε την κατανομή της απόστασης πομπού-δέκτη. Στο σχήμα 1 δίνεται η θεωρητική PDF και το ιστόγραμμα με προσομοίωση της απόστασης πομπού-δέκτη με βάση το RWP model για D=100m.
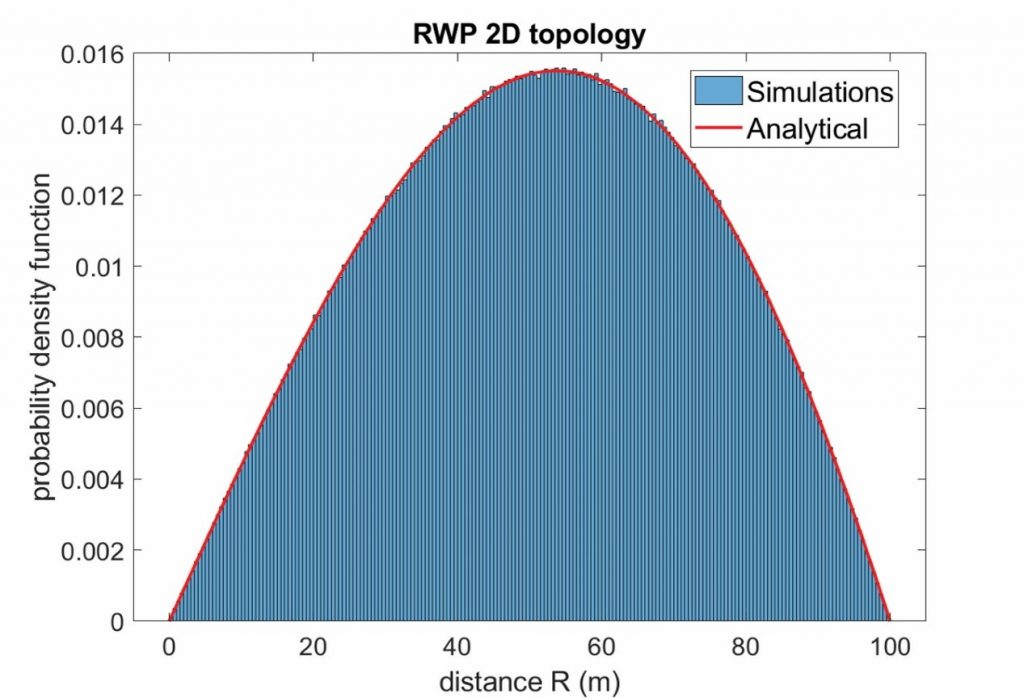
Η διαφορά με τον ακίνητο δέκτη είναι ότι τώρα η μέση λαμβανόμενη ισχύς (άρα το μέσο λαμβανόμενο SNR) είναι τυχαία μεταβλητή με PDF η οποία υπολογίζεται με βάση την PDF της απόστασης πομπού-δέκτη R, όπου 0<R<D. Επομένως πρέπει να υπολογίσουμε το στατιστικό μέσο όρο της χωρητικότητας του καναλιού με διάλειψη για σταθερό μέσο SNR ως προς την κατανομή (PDF) του μέσου SNR, αφού το μέσο SNR συνεχώς μεταβάλλεται για τον κινούμενο δέκτη όπως μετακινείται μέσα στην περιοχή κάλυψης.
Στο άρθρο αυτό δίνουμε μαθηματικές σχέσεις για τη χωρητικότητα κατά Shannon (ergodic capacity) για έναν κινούμενο δέκτη μέσα σε μία περιοχή κάλυψης με ακτίνα D συναρτήσει του μέσου SNR στο όριο της περιοχής κάλυψης SNR_D. Επίσης συγκρίνουμε την χωρητικότητα του κινούμενου δέκτη με έναν δέκτη που βρίσκεται στη μέση της περιοχής κάλυψης (απόσταση πομπού-δέκτη d=D/2). Τέλος δίνουμε ασυμπτωτικές μαθηματικές σχέσεις της χωρητικότητας για μεγάλες τιμές του μέσου SNR_D, οι οποίες μας δείχνουν την επίδραση των παραμέτρων της διάλειψης του καναλιού αλλά και των παραμέτρων της κίνησης του δέκτη στη χωρητικότητα που μπορούμε να πετύχουμε.
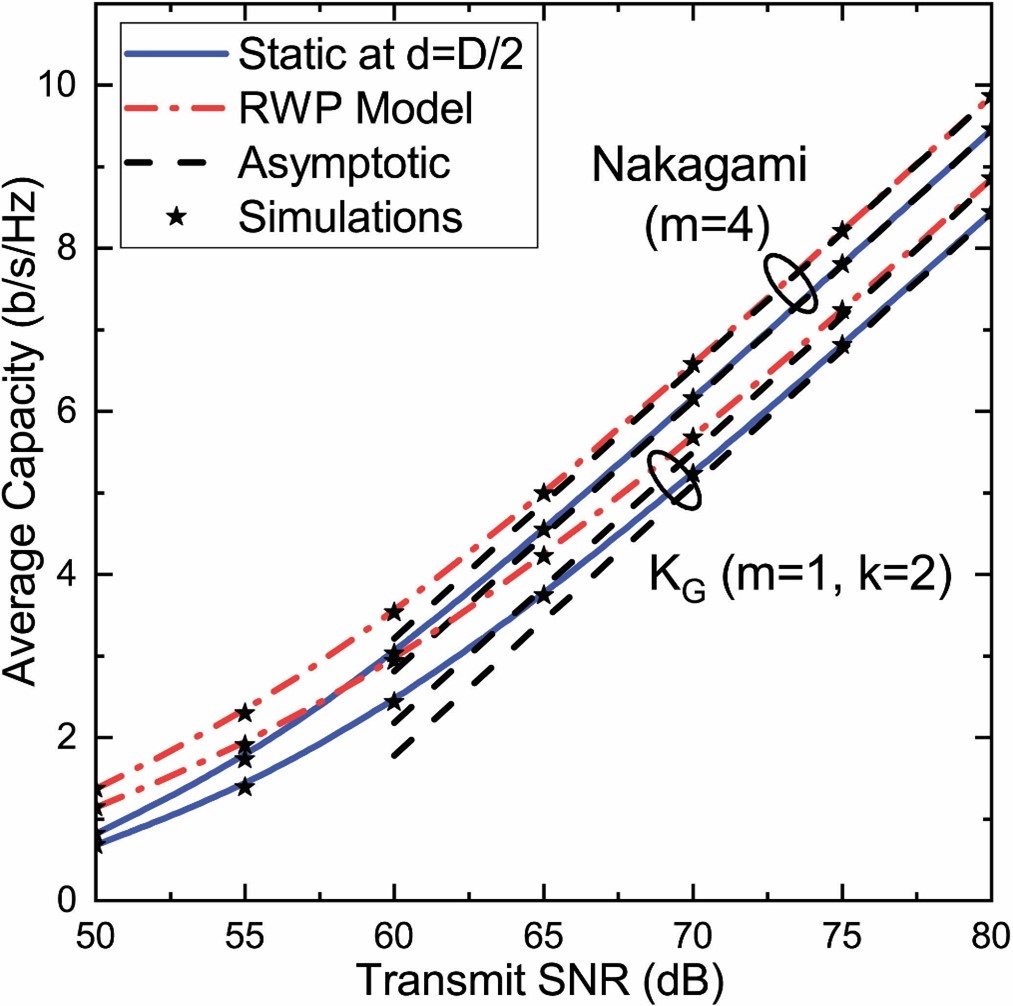
Στο Σχήμα 2 δίνεται η χωρητικότητα του καναλιού συναρτήσει του transmit SNR=P_t/N για δύο στατιστικές διάλειψης: Nakagami-m και Generalized-K, για στατικό δέκτη σε απόσταση d=D/2 και για κινούμενο δέκτη με το μοντέλο RWP. Τέλος, επειδή η χωρητικότητα του κινούμενου δέκτη υπολογίζεται ως η στατιστική μέση τιμή σε πολλές αποστάσεις πομπού-δέκτη, μπορεί να θεωρηθεί και ως η μέση φασματική απόδοση (average spectral efficiency) μέσα στην περιοχή κάλυψης. Αυτή είναι μία πολύ σημαντική παράμετρος στο σχεδιασμό των δικτύων διότι όταν πολλαπλασιαστεί με το φάσμα εκπομπής ενός σταθμού βάσης δίνει την μέση προσφερόμενη χωρητικότητα σε bit/sec που μπορεί να προσφέρει ο σταθμός βάσης που βρίσκεται στο κέντρο μίας περιοχής κάλυψης με ακτίνα D.
REFERENCES
[1] D. B. Da Costa and M. D. Yacoub, “Average channel capacity for generalized fading scenarios,” IEEE Commun. Lett., vol. 11, no. 12, pp. 949–951, Dec. 2007.
[2] K. Govindan, K. Zeng, and P. Mohapatra, “Probability density of the received power in mobile networks,” IEEE Trans. Wireless Commun., vol. 10, no. 11, pp. 3613–3619, Nov. 2011.
[3] V. A. Aalo, C. Mukasa, and G. P. Efthymoglou, “Effect of mobility on the outage and BER performances of digital transmissions over Nakagami-m fading channels,” IEEE Trans. Veh. Technol., vol. 65, no. 4, pp. 2715–2721, Apr. 2015.
[4] V. A. Aalo, P. S. Bithas, and G. P. Efthymoglou, “On the impact of user mobility on the performance of wireless receivers,” IEEE Access, vol. 8, pp. 197300–197311, Oct. 2020.
Άρθρο:
Θέση εργασίας στην εταιρεία Contships Management Inc.: Junior IT-ERP Operator
Σύντομη περιγραφή αρμοδιοτήτων:
- Εγκατάσταση και παραμετροποίηση Η/Υ
- Επίβλεψη και παραμετροποίηση: δικτύων, συστημάτων Servers, VSphere, VOIP, Δορυφορικών συστημάτων.
- Επίβλεψη και υποστήριξη στο ERP (Danaos) σύστημα της εταιρείας
Email επικοινωνίας: erp@contships-management.com
Σίτιση φοιτητών/τριών ακαδημαϊκού έτους 2022-2023 (πρωτοετείς)
Αιτήσεις από 5 Οκτωβρίου 2022 έως 25 Οκτωβρίου 2022
Δείτε πληροφορίες εδώ.

